斑图动力学
探索自然界中模式形成与演化的数学原理
斑图动力学是研究复杂系统中自发形成的空间结构和时间演化模式的科学,涉及数学、物理、化学和生物学等多个领域。
斑图动力学概述
斑图动力学(Pattern Dynamics)是研究复杂系统中自发形成的空间结构和时间演化模式的跨学科领域。它探索自然界中各种规则和不规则模式的形成机制,从动物皮毛的条纹到化学反应中的螺旋波,从沙漠沙丘到大脑神经活动。
这一领域起源于1952年艾伦·图灵的开创性论文《形态发生的化学基础》,他提出反应-扩散机制可以解释生物模式的形成。此后,斑图动力学逐渐发展成为连接数学、物理、化学和生物学的桥梁学科。


图灵斑图
由艾伦·图灵提出的反应-扩散模型可以解释自然界中许多重复模式的形成,如斑马条纹和豹斑。
反应-扩散系统
化学物质通过反应和扩散过程形成复杂空间模式的基本机制,如Belousov-Zhabotinsky反应。
细菌菌落模式
微生物在受限环境中生长时形成的复杂分形结构,展示了生物系统中的自组织现象。
基本原理与概念
斑图动力学建立在几个基本概念之上,这些概念解释了简单规则如何产生复杂模式:
自组织
系统在没有任何外部控制器的情况下,通过局部相互作用自发形成有序结构的过程。例如:鸟群的形成、晶体生长、雪花形成。
对称破缺
系统在临界点失去对称性,从而产生空间模式的过程。均匀状态变得不稳定,导致模式出现,如Bénard对流胞。
波与振荡
时空模式中常见的波动现象,如靶波、螺旋波和振荡模式,常见于心脏组织、化学振荡反应和萤火虫同步闪光。
分形结构
在不同尺度上具有自相似性的复杂几何形状,如海岸线、肺支气管结构、河流网络和神经网络。

非线性动力学
斑图形成的核心是非线性动力学:系统中微小的变化可能导致巨大的、非比例的结果。这种非线性特性使得系统能够从均匀状态自发演化出复杂的空间模式。
典型的非线性系统包括:
- 反应-扩散系统
- 耦合振荡器
- 流体动力学系统
- 神经动力学网络
数学模型
斑图动力学使用多种数学工具描述和预测模式的形成与演化:
反应-扩散方程
描述物质浓度如何随时间变化并在空间中扩散的基本方程:
∂v/∂t = Dv∇²v + g(u,v)
其中 u 和 v 代表化学物质浓度,D 是扩散系数,f 和 g 表示局部反应动力学。
图灵不稳定性
当满足以下条件时,均匀稳态会变得不稳定,导致空间模式的形成:
其中 fu, fv, gu, gv 是反应函数在稳态处的偏导数。
数值模拟方法
由于大多数斑图动力学方程没有解析解,数值方法成为研究这些系统的重要工具:
- 有限差分法:将空间和时间离散化求解偏微分方程
- 元胞自动机:基于简单规则的离散空间模型
- 粒子方法:追踪系统中每个粒子的运动
- 谱方法:利用傅里叶变换求解空间导数
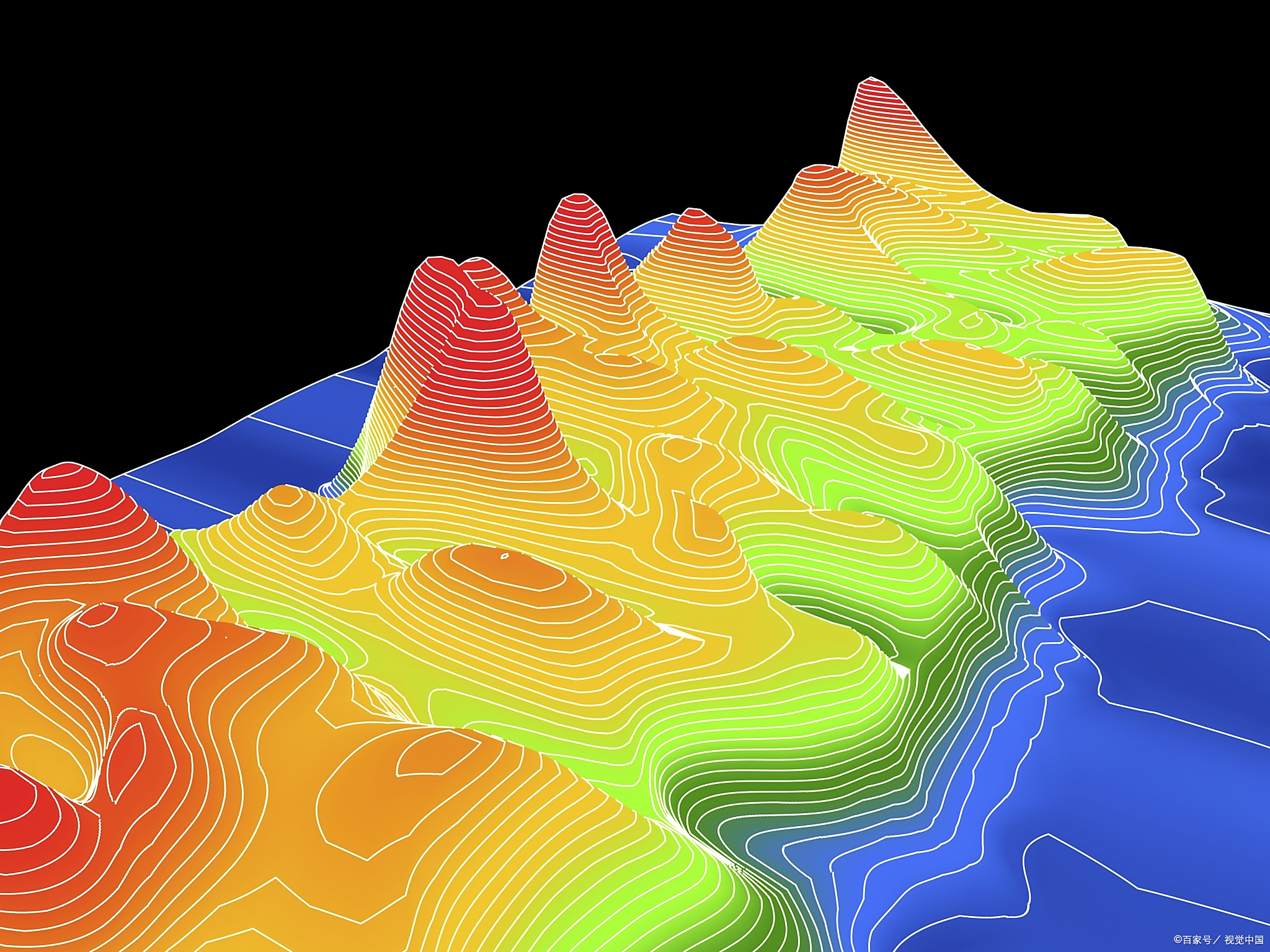
斑图动力学模拟
通过改变参数观察不同类型的斑图形成:
Gray-Scott模型
当前模拟使用Gray-Scott模型,该模型描述了两种化学物质的反应扩散过程:
∂v/∂t = Dv∇²v + uv² - (F + K)v
其中u和v是化学物质浓度,F是供给速率,K是消耗速率。通过调整这些参数,可以产生斑点、条纹、迷宫等多种模式。
应用领域
斑图动力学在多个科学领域有重要应用:
发育生物学
解释动物皮毛图案、肢体发育和器官形成过程中的模式形成机制,理解形态发生的原理。
化学与材料科学
理解BZ反应等化学振荡器以及材料自组装过程中的图案形成,设计新型功能材料。
神经科学
研究大脑皮层活动模式、癫痫波传播和神经发育中的模式形成,理解脑功能与疾病。
生态学与地貌学
解释植被分布模式、沙漠沙丘形成和地质结构中的规则图案,预测环境变化。

前沿研究与未来方向
斑图动力学正在多个前沿领域展现出巨大潜力:
- 合成生物学:设计具有特定模式的工程生物系统
- 活性物质:研究自驱动粒子系统的集体行为
- 人工智能:受生物模式启发的神经网络结构
- 医学应用:基于模式理论的疾病诊断和治疗
- 气候科学:理解全球气候模式的形成与演化